刘志文,王进强,b,王广鑫
(北京科技大学 a.土木与资源学院,b.金属矿山高效开采与安全教育部重点实验室,北京 100083)
地震P波到时拾取是地震数据处理中关键的一环,拾取效率与精度直接影响震源定位的效率和精度。随着数字地震台网的大量建设,海量测震数据的产生,人工拾取P波不仅费时费力,还难以进行快速智能预警,自动化快速精确识别震相对于地震学的研究有着重要的意义[1]。传统的STA/LTA(长短时窗均值比法)[2]方法虽然过程简单,但精度不够,对低信噪比的数据拾取效果不好,且阈值需要自己设定;
利用AIC(赤池信息准则)[3]来寻找全局极小值作为P波初至,虽然效果要比STA/LTA好,但是计算复杂,对低信噪比数据的拾取效果不理想。1985年MAEDA提出M-AIC[4],可跳过AR系数计算,直接用地震数据计算信号的AIC值。1999年SLEEMAN提出AR-AIC[5]模型用于震相的拾取,效果比STA/LTA好,但是依赖于时窗长度和AR系数的设定,也存在对低信噪比数据拾取效果不理想的情况。
语义分割是深度学习的一个研究领域,其将图片中的每个像素点进行预测分类,并将每个类别的边缘标注出来用不同的颜色对不同类别进行填充,从而达到边缘检测和分类的目的。将地震P波初至自动拾取问题看成一个二分类的问题(是否为P波初至),需要判断地震序列中的每个采样点是否是P波初至。因为这一判断和语义分割问题类似,因此可以借鉴语义分割模型对P波初至进行自动拾取研究。FCN(全卷积网络)、U-Net(U型网络)、UNet++、DeepLabV3都是很好的语义分割模型,在图像处理方面取得了很好的效果。FCN是语义分割模型的先驱,它的结构全部由卷积层组成,所以叫全卷积网络,其将来自深层、粗略层的语义信息与来自浅层、精细层的外观信息相结合,以产生准确和详细的分割[6]。U-Net形状类似字母U的形状,所以叫U型网络,它通过下采样抓住上下文的信息得到高级语义特征图,再通过上采样将图片恢复到原分辨率进行输出[7]。ZHU et al[8]基于U-Net网络进行改进,提出了PhaseNet,相比于原始的U-Net网络结构,PhaseNet每个水平层都少了一个卷积层。PhaseNet对P波初至拾取的准确率达到了93.9%,远高于AR-AIC 55.8%的准确率,其对地震震相的高精度识别验证了U型网络可以很好地应用到地震P波初至的自动拾取上。赵明等[9]基于U-Net网络提出了U型网络对震相的拾取,将U-Net中加入了Dropout层,能有效防止模型过拟合,但拾取精度不佳。MOUSAVI[10]提出了EQT模型用于地震事件检测和震相拾取,EQT模型包括多层卷积池化层、残差网络层、双向LSTM层、LSTM层、Transformer层,最后将其分成三部分,用于检测地震事件、P波到时、S波到时。P波到时预测的这一部分包括一层LSTM、局部注意力机制和多个上采样、卷积操作,最后经过Sigmoid层输出P波概率分布。虽然EQT在拾取精度上很高,但是该模型庞大臃肿、参数量太多,耗费计算资源也更大。
UNet++是基于U-Net改进的一种神经网络结构,在语义分割的任务上的表现比U-Net好,主要是它整合了不同层次的特征,比U-Net增加了更多的特征拼接操作。理论上可以利用UNet++模型进行地震P波拾取,但相关研究未见报道。本文首先对UNet++网络结构进行改造,然后进行地震波到时拾取研究,并与传统方法进行对比,验证本文方法的可行性与优越性。
UNet++是一个基于嵌套密集的跳跃连接的语义分割模型,结构背后的基本假设是:当来自编码器网络逐渐丰富的高分辨率特征图在与来自解码器网络的相应语义丰富的特征图融合之前,该模型可以更有效地捕捉对象的细粒度细节[11]。
为了使UNet++能应用于地震P波初至拾取,且达到很好的效果,本文基于原始网络结构在3个方向进行了改进:网络降维、改变单个Block中的操作和改变网络的深度。
为了验证单个Block中的操作对模型效果的影响,首先在保持原始网络深度不变的情况下,改变单个Block中的操作,有增加或者减少单个Block中一组卷积和样本归一化操作的选择,对比不同情况下在验证集上漏拾数、正确拾取数、误拾数的变化,实验结果见表1.从表1可知增加一组操作,在误拾取和正确拾取数上的结果优于不变和减少一组操作。虽然漏拾数比减少一组效果差,但从整体上来考虑,增加一组操作的效果明显更好。结果也可以用理论来解释,增加一组卷积和样本归一化操作,可以使神经网络输出更多的特征通道数,学到更多的地震P波特征,因此拾取P波的效果也更好。
确定每个Block中的操作后,再确定网络结构的深度,分别做三组实验,在3、4、5层网络深度的情况下,网络在验证数据集上的表现,得到的结果如图1所示。
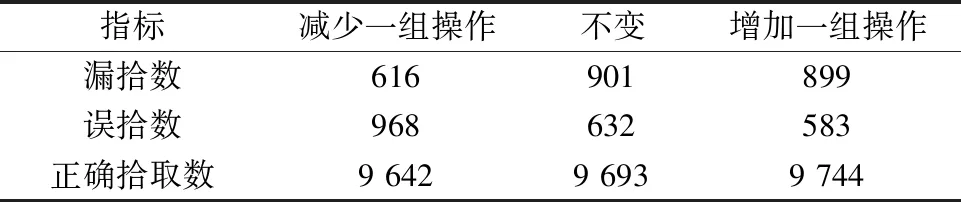
表1 改变单个Block中的操作模型在验证集上的表现Table 1 The validation set upon the change in the operation model in a single Block
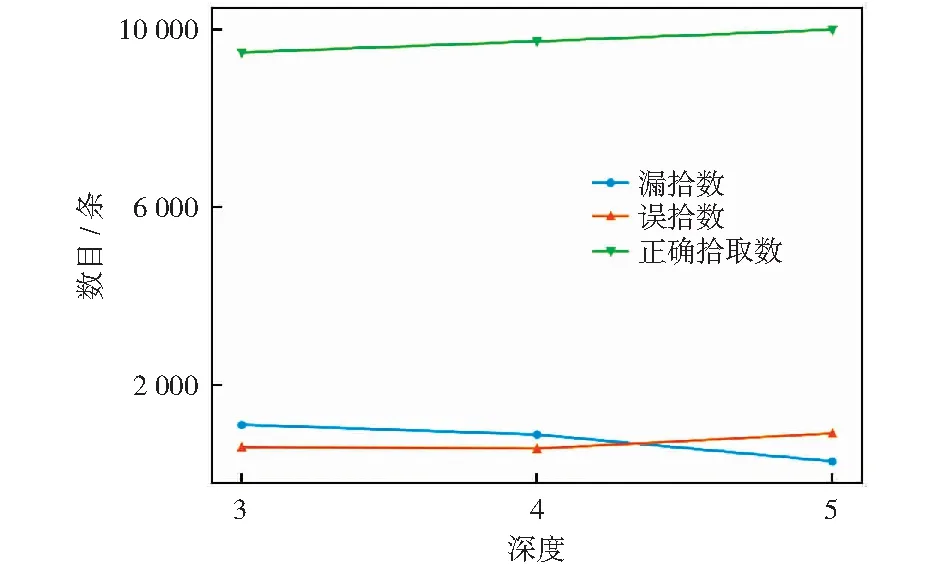
图1 不同网络深度模型在验证集上的表现Fig.1 Performance of different network depth models on the validation set
从图1可以看出随着网络深度的增加,正确拾取数逐渐增加,漏拾数逐渐减少,误拾数不是在网络深度为5时表现最优。虽然误拾数是在网络深度为4时表现最优,但考虑到模型的任务主要是得到更多的正确拾取数,所以网络深度确定为5层。
最终确定本文模型结构如图2所示。图中每个Block中的操作都一样,Conv1、Conv2、Conv3都是一维卷积,卷积核大小为3,步长为1,填充为1,这样做是为了使卷积后得到的结果和一维地震序列的长度保持一样。样本归一化(Batch Normalizaion)操作有助于防止模型过拟合,其效果比添加Dropout层要好[12]。ReLU增加了神经网络各层之间的非线性关系,且可以缓解梯度消失;
池化操作(即下采样)为最大池化,核大小为2,步长为2,经过池化后的数据长度会减半;
上采样操作的缩放因子为2,将下采样后的样本恢复到原长度,插值方式为线性插值。跳跃连接将每个Block得到的输出在特征维度上进行向量的拼接。网络结构中第一个Block接收地震数据的输入,输入的向量维度为(B,3,6 000),B表示样本批次大小,本文中取64,最后一个Block的输出再经过一次一维卷积得到预测结果,输出结果的向量维度为(B,2,6 000).

图2 本文模型网络结构图Fig.2 Network structure diagram of the model in this paper
综上,本文模型和UNet++不同之处有:1) 维度不同,UNet++是二维图像的语义分割模型,地震数据是一维时间序列数据,不能直接用于地震P波的拾取。对其进行降维,卷积、池化、批次归一化都降为一维操作;
2) 网络结构的深度不同:原始网络深度为4层,本文模型为5层;
3) 每个Block中的操作不同:原始网络中每个Block包含Conv1(卷积1)、BN1(批次归一化1)、Conv2(卷积2)、 BN2(批次归一化2)、ReLU的操作,本文模型多了一组卷积和批次归一化操作。
在本文中将微震P波自动拾取看作一个二分类问题,损失函数选取交叉熵损失(CrossEntropyLoss),公式如下:
(1)
式中:N为微震序列信号长度,yij是二值化编码标签,i=1,2表示有两个类别分别为P波初至和非P波初至,其表达式为:

(2)
其中,z为最后一层输出的张量,形状大小为(m,2,N),m为样本批次大小。
深度学习中常用的优化器有SGD(随机梯度下降)、Momentum、RMSprop[13]、Adam等,本文中的模型使用的是Adam,Adam优化器是Momentum和RMSprop的结合,能很快地找到正确方向并前进,且收敛速度快,可以让模型更快地到达全局最优值。
训练、验证、测试数据均来源于STEAD[14](斯坦福地震数据集),数据集的Github地址为https:∥github.com/smousavi05/STEAD,从该地址下载好需要的数据集。从源数据中筛选出三通道信噪比都低于某个值的数据,这里选择低于20 dB的数据。选择低信噪比的数据的原因是:高信噪比数据的P波自动拾取传统算法就能做得很好,对低信噪比数据进行P波自动拾取研究更有意义。选出小于20 dB的数据共56 130条,每条数据长度都为6 000,采样频率为100 Hz.原始数据示例见图3(a),从图中可以看出信号信噪比低,噪声和有效信号混叠在一起,很难快速准确地确定P波初至点。
为了减少噪声对模型的干扰,让模型更好地学习P波波形特征,对原始波形数据进行降噪处理。目前,广泛使用的微震信号降噪方法主要有以下几类:1) 利用有效波和噪声的频率差异去噪;
2) 利用有效波和噪声的传播方向 (视速度) 差异去噪;
3) 利用有效波和噪声的空间分布差异去噪;
4) 利用微地震资料的区域统计差异去噪;
5) 利用信号间的相干性区分噪声;
6) 基于神经网络的微地震去噪方法[15]。本文中用到的地震数据震级大部分比2.5M小,为微震事件。针对微震信号的随机非平稳性,降噪方法选取第三类中的小波阈值滤波法。小波阈值法是以小波变换理论为中心发展而来的,小波变换在信号的低频部分具有良好的频率分辨率,在高频部分具有良好的时间分辨率[16-17]。利用这一优势,DONOHO et al[18]提出一种基于小波变换的小波阈值滤波算法,TO et al[19]将其应用于微震信号降噪方面,并与维纳滤波法进行对比,证明了这种方法可以用于微震信号降噪。阈值函数选择软阈值,硬阈值函数存在不连续点,易出现伪吉布斯点,选择软阈值函数使降噪后的信号更平滑;
阈值选取为固定阈值,用固定阈值或启发式阈值进行降噪与选极大极小阈值或无偏风险估计阈值进行降噪相比,前者的降噪效果比较彻底,而后者相对保守,前者降噪效果好。在微震信号降噪时,采用固定阈值或启发式阈值降噪比较完全,更为有效[20];
小波函数选择的是Sym8,Sym8小波基函数与地震信号的特征类似,有更好地提取微震信号的能力,降噪效果更好。通常小波分解的频段范围与采样频率有关,若N层分解,则各个频段大小为Fs/2/2N[21].当小波函数和采样周期选定之后,信号多分辨率分解的各层所占的频带是一定的,将各层频带与实际信号的有效频带相比较,就可以确定小波分解层数[22]。经计算分解层数为6,过大则会造成信号失真。最后对经小波阈值去噪后的波形进行归一化处理,得到的数据如图3(b)所示,从图中可以明显看出P波初至点,去噪效果好,并且对数据进行归一化后,减少了不同振幅大小对模型特征学习的干扰。

图3 数据降噪前后对比Fig.3 Comparison before and after data noise reduction
将数据集中实际P波到时的前后25个点都标注为1,其余标注为0.选前后25个点的原因是人工拾取的P波到时存在-0.25~0.25 s的误差,本文数据采样频率为100 Hz,所以是前后25个点。图4是将图3(b)中Z分量数据进行标注处理前后的对比图(为了让P波初至和非P波初至标签对比明显,截取了前20 s的数据),P波到时为7 s.

图4 数据标注前后对比Fig.4 Before and after data labeling
将数据预处理好后,按照4∶1的比例划分训练集和验证集,训练数据有44 904条,验证数据有11 226条。
用Pytorch框架搭建本文模型网络结构,并在Kaggle(谷歌提供的虚拟机)上训练和验证,Kaggle配置为16G的运行内存,73G储存,GPU为Tesla P100,最大功耗300 W.训练和验证样本都按批次输入到模型,每个批次的大小为64条原始数据,训练和验证的轮数为5,总共花了70 min.喂入一个批次进行训练就是1个Time step(时间步),总共有3 510个Time step,每轮有702个Time step,每50个Time step记录一次损失函数的值。
每轮训练完再喂入验证数据集进行验证,得到模型在验证集上的表现,绘制其精确度和召回率随训练轮数变化的图像,如图5(b)所示。由于训练数据庞大,模型在第一轮训练后几乎已经收敛,验证集上数据的精确率和召回率不随训练轮数增加有明显的增加,并且有时呈现下降的趋势,但精确率基本维持在93.1%~94.3%之间,召回率在87%~92.2%之间。从图5(a)中可以看出,继续增加训练轮数,训练集上的损失值还会继续下降,但下降幅度微小,在一个微小的区间内震荡,趋于平稳,对精确率和召回率的提升可以忽略。由图5(b)可知在第一轮训练后,验证集上的精确率就已经达到93.1%,第二轮继续提升,之后三轮保持稳定。召回率在第一轮训练后达到89.6%,第二轮有所下降,之后三轮缓慢攀升,有趋于稳定的态势。综上,选择第5轮的模型作为最终模型,其在验证集上精确率和召回率分别为94%、92.2%.

图5 模型训练与验证过程Fig.5 Model training and verification process
测试数据集的信噪比也是低于20 dB,且经过和训练、验证数据一样的处理,一共有150条。为了客观评估本文网络模型在测试集上的表现,我们选取了2种常用的震相拾取算法进行对比:STA/LTA和AR-AIC,对于3种方法的检测结果,以人工到时拾取结果为标准,保证结果的可靠性。为评估3种方法的表现,使用平均值(μ)、方差(δ)、精确率(H)、召回率(R)作为评价指标,4个指标计算公式如下:
(3)
(4)
(5)
(6)

分别计算3种方法在测试集上得到的4个指标的值,结果见表2.其中STA/LTA和AR-AIC用的是Obspy(处理微震数据的Python库)中的算法,代码在本机中实现。在Obspy中,STA/LTA法拾取P波初至需传入的参数为长短时窗宽度;
AR-AIC法拾取P波初至需传入的参数为低通频率、高通频率、长短时窗宽、AR系数和时窗方差。

表2 本文模型与STA/LTA、AR-AIC算法对比Table 2 Comparison of the model in this paper with STA/LTA and AR-AIC algorithms
从表2中可知, 本文模型在测试集上的精确率是98.00%,比STA/LTA高32%,比AR-AIC高22%,测试集数据信噪比大部分都低,如果数据信噪比高一些,精确率还会更高。平均值反映方法正确拾取P波时与人工拾取误差绝对值的平均值,方差则反映方法正确拾取时,每次的拾取误差绝对值和总体拾取误差绝对值的平均值的分布是否集中,这两个值都是越小越好。从表2中可知本文模型要优于AR-AIC,AR-AIC要优于STA/LTA.因为测试的样本比较少,所以3种方法在召回率的表现上都为1,没有漏拾的情况。
本文模型在150条测试数据上的表现:147条数据正确拾取,3条数据错误拾取(误差分别为0.625 s、0.91 s、-1.06 s),0条漏拾。为了观察模型正确拾取时与人工拾取的误差分布,绘制直方图如图6所示,从分布上来看大部分误差集中在0~0.05 s,说明模型的拾取精度高,完全可以代替人工拾取。
图7给出了本文模型在不同信噪比下与人工拾取的结果对比。图7(a)中的数据虽然经过小波阈值去噪信噪比有所提高,但是起跳点依然不明显,本文模型能够无误差地拾取P波到时;
图7(b)中本文模型拾取到时与人工拾取到时相差0.1 s,说明本文模型拾取延后;
图7(c)中本文模型拾取到时与人工拾到时相差-0.215 s,说明本文模型过早拾取;
图7(d)中本文模型拾取到时与人工拾到时相差0.625 s,模型拾取错误;
图7(b)、(c)中本文模型拾取结果和人工拾取结果误差小,从图中看两条线重合在一起,将其部分放大才能看出差距,放大后见图8(a)、(b).

图6 模型拾取正确时与人工拾取到时的误差分布Fig.6 Error distribution when the model is picked correctly and when it is picked manually

图7 本文模型在不同信噪比下与人工拾取的结果对比Fig.7 Comparison of the model in this paper with the results of manual picking under different signal-to-noise ratios
从图7(d)中可以观察出对于信噪比太低的数据,P波起跳点被噪声所淹没,本文方法依然能够进行到时拾取,但误差较大。对于这种数据可以看看其它通道有没有更好的数据或者改进去噪算法,让P波起跳点更明显,达到拾取P波初至的目的。
为了验证模型的泛化能力,对输入数据进行加噪处理,得到的预测结果和未加噪的数据进行对比,如图9所示。图9中实际P波到时是8 s,模型对未加噪数据的预测结果为8 s,对加噪10%数据的预测结果为8.01 s,可见模型对于加噪后的数据仍然能以很小的误差拾取P波初至,表明模型泛化能力强。
PhaseNet和EQT是两种先进的震相拾取深度学习模型,得到了广泛的关注和初步的应用[23]。在P波初至拾取精度上PhaseNet达到了0.96,EQT为0.99[10],本文模型为0.98.本文模型和PhaseNet在结构上存在很大的差异,本文模型增加了同层之间的残差连接,从第二层开始就进行了上采样,更多的残差连接有助于避免训练过程中的梯度消失问题,而从第二层开始上采样能抓住不同层次之间的特征,让网络自己去学习不同深度的特征,因此在P波初至拾取精度上本文模型更好些。EQT模型庞大,有很深的网络结构,需要训练的参数量多,可能会造成模型过拟合,本文模型参数量与之相比要少很多,训练所花费的资源比EQT模型少,但本文模型几乎能达到和EQT同样的P波初至拾取精度,因此本文模型具有良好的应用价值。

图8 图7(b)、(c)部分放大图Fig.8 Enlarged view of part (b) and (c) of Fig. 7

图9 模型泛化能力验证Fig.9 Validation of model generalization ability
1) 三种方法在测试集上的表现证明本文模型在P波初至拾取上明显优于STA/LTA和AR-AIC方法,可以替代传统P波自动拾取方法。
2) 模型训练需要花较长的时间,依据训练好的模型进行单个数据预测,耗时可以忽略不计(小于1 s),能够满足实际需求。
3) 使用训练好的模型对加噪后的数据进行测试,模型也能很好地拾取,验证了本文模型泛化能力较好。
4) 面对日益增多的地震数据,每条数据的P波初至都由人工拾取显得很不合理。本文将深度学习模型UNet++用于地震数据的P波初至拾取,取得了很好的效果,对推进深度学习在P波初至自动拾取上的应用有较强的现实意义。
猜你喜欢集上信噪比卷积两种64排GE CT冠脉成像信噪比与剂量对比分析研究现代仪器与医疗(2022年1期)2022-04-19基于3D-Winograd的快速卷积算法设计及FPGA实现北京航空航天大学学报(2021年9期)2021-11-02Cookie-Cutter集上的Gibbs测度数学年刊A辑(中文版)(2020年2期)2020-07-25链完备偏序集上广义向量均衡问题解映射的保序性数学物理学报(2019年6期)2020-01-13基于深度学习的无人机数据链信噪比估计算法北京航空航天大学学报(2019年9期)2019-10-26分形集上的Ostrowski型不等式和Ostrowski-Grüss型不等式井冈山大学学报(自然科学版)(2019年4期)2019-09-09从滤波器理解卷积电子制作(2019年11期)2019-07-04基于傅里叶域卷积表示的目标跟踪算法北京航空航天大学学报(2018年1期)2018-04-20低信噪比下基于Hough变换的前视阵列SAR稀疏三维成像雷达学报(2017年3期)2018-01-19保持信噪比的相位分解反褶积方法研究西南石油大学学报(自然科学版)(2015年5期)2015-04-16扩展阅读文章
推荐阅读文章
恒微文秘网 https://www.sc-bjx.com Copyright © 2015-2024 . 恒微文秘网 版权所有
Powered by 恒微文秘网 © All Rights Reserved. 备案号:蜀ICP备15013507号-1