基于残差矩阵SVD的混凝土梁超声信号温湿度干扰去除算法

郑罡，陈伟基，陈鹏，彭宇

重庆交通大学省部共建山区桥梁及隧道工程国家重点实验室，重庆 400074

超声波在混凝土结构传播时受材料非均匀性影响，会发生多次散射、衍射与折射现象，由此形成的尾波蕴藏着丰富的介质变化信息，这一特点使得尾波逐渐成为近十余年来测量评估混凝土结构应力领域的研究热点[1-3]。研究表明，尾波干涉测量混凝土结构应力的分辨率可达0.01～0.1MPa[4-6]，然而在实际测量中，尾波的高灵敏性也意味着应力测试评估结果易受温湿度等环境因素不同程度的干扰[7-11]。尤其是环境温度变化的影响，温度变化会导致材料的几何形状和弹性模量发生改变，从而导致超声波波速变化，评估结果发生改变，在大多数情况下这种影响是不利的[8]。因此，有必要去除温湿度等环境因素对结构超声测试结果的影响[12]。

目前，已有学者针对该问题展开了研究，以下2种方法较为典型。方法一，热补偿技术，测试样本承受与参考样本相同的温度变化，通过使用参考样本补偿由温度变化引起的尾波干涉测量结果的波动[13,14]。方法二，最优基线选择法，事先存储不同环境情况下的基线数据，然后评估选取出与新测量波形最相似的基线，调整该基线，计算信号与调整后的波形之间的误差参数，将该参数与阈值进行比较以确定结构状态[15-17]。上述2种方法均取得较好的理论效果，但实际测试中，这些方法的应用常受参考样本缺失[14]、大型数据库建立困难[16]等问题制约。因此，为规避上述困难，推动超声尾波测量结构应力领域向工程应用靠近，研究发展新技术是必要的。基于前期取得的混凝土超声应力测试经验[18-20]，笔者进一步探明超声测试的干扰来源，并针对性地建立算法去除信号中环境温湿度干扰成分，获得稳定性较好的超声尾波信号，为后续混凝土结构应力测量方法的研究创造条件。

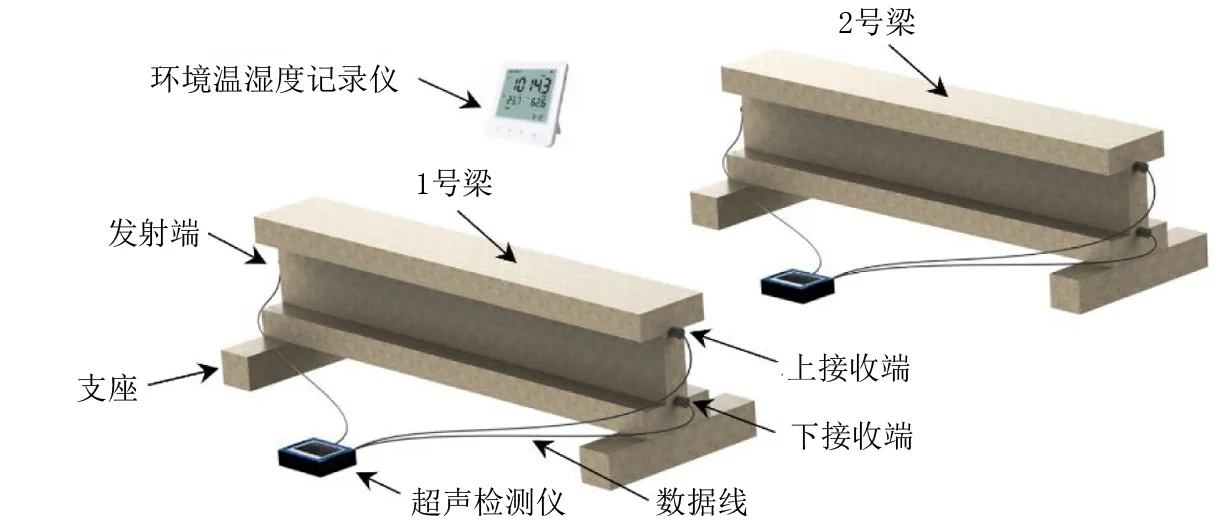
图1 试验系统总体布置示意图Fig.1 General layout diagram of the test system

为探究环境条件对混凝土超声测试的影响，借鉴文献[14,18]的试验方案，在环境温湿度自然变化的室内条件下，同时开展两片试验梁的超声尾波测试，两片试验梁放置在邻近位置，梁体均处于自重状态，可认为处于无荷载扰动状态。试验系统主要由试验梁和测试系统两部分组成，图1为试验系统总体布置示意图。

1.1 试验梁

笔者所采用试验梁为文献[18]中同批次浇筑的两片钢筋混凝土工字梁，分别命名为1号梁、2号梁。工字梁梁长200cm，梁高45cm；
顶底板宽30cm，厚10cm；
腹板高25cm，厚10cm。混凝土标号为C30，配筋构造如图2所示。

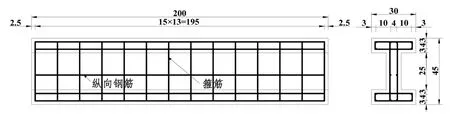
图2 工字梁配筋图(单位：cm)[18]Fig.2 Reinforcement diagram of I-beam (unit:cm)[18]

1.2 测试系统

测试系统包括超声测试系统和环境温湿度记录仪。

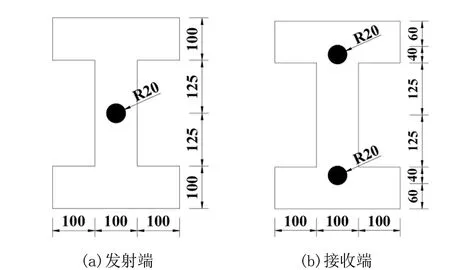
图3 换能器布置图(单位：mm)Fig.3 Transducer layout (unit:mm)

其中，超声测试系统由RSM-SY5(T)非金属声波检测仪、JHP01型换能器、数据线和环氧树脂耦合剂等设备构成。采用环氧树脂固定可避免由于换能器耦合条件的变化而影响信号的稳定性[18]。每片试验梁均选择一发双收采集超声尾波信号，发射端的换能器布置于梁一端横截面中心，两个接收端的换能器则对称布置于梁另一端横截面对称轴的上下部，如图3所示。此外，根据文献[18]的仪器参数设置，经过多次反复调试，确定了该试验中声波检测仪中采样点数、采样间隔与增益等6个仪器关键参数，具体参数如表1所示。

环境温湿度记录仪采用YEM-70L环境温湿度自动记录仪。

表1 声波检测仪参数设置

1.3 试验数据采集

为使得试验结果可进行相互验证，在同一环境温湿度变化区间内对两片试验梁均进行两组超声测试试验，每组试验进行14d。考虑获得更多信号样本，每天进行14个连续时段的超声测试，每时段内仪器将自动完成400次采集，一次采集得到1条含1024点的超声尾波信号。此外，每天试验测试前均对超声测试仪器进行1h预热工作，待仪器示值稳定时再进行正式测试[18]。超声测试时记录环境温湿度，记录频次为每5min一次。

2.1 数据预处理

每片试验梁采集得到的数据均进行以下预处理：①计算得到单天平均超声数据；
②每条单天平均数据进行零均值化；
③每条单天平均数据再进行归一化。预处理后，每组试验的每个接收端均可得到14条单天样本数据。

由于同一片试验梁体上下两个接收端的数据处理分析结果基本一致，文中仅以上接收端的数据为例进行讨论分析。

2.2 信号波动评估

每条超声尾波数据均可看成1024维的空间列向量，本文利用方向余弦导出归一化夹角反映数据之间的相似性，以此评估测试信号的波动状况。设wi、wj为预处理后的任意两条尾波数据，两者的方向余弦夹角由下式得：

(1)

2.3 基于残差矩阵SVD(奇异值分解)的信号环境干扰去除算法

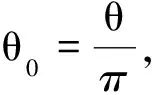
2.3.1 残差矩阵SVD

设测试得到n条m维的超声数据，对其进行零均值化和单位化处理，并将其组成矩阵，记为测试信号矩阵Wm×n=[w1,w2,…,wn]。再将Wm×n中n条数据的平均数据进行单位化，记为参考信号w0。

构造残差矩阵Wv，即Wm×n中每条数据均减去其在参考信号w0上的投影，意为测试信号与参考信号的偏差：

Wv=[w1-cos(w1,w0)×w0,w2-cos(w2,w0)×w0,…,wn-cos(wn,w0)×w0]

(2)

式中:cos(wn,w0)为wn与w0的方向余弦。

对残差矩阵Wv进行SVD，得：

Wv=UΣVT

(3)

式中:T表示转置运算；
U和V分别为m×m和n×n的正交矩阵。U的列向量为奇异值中的左奇异向量，其组成了m维空间的一组标准正交基，即U=[u1,u2,…,um]，文中该列向量视为信号中干扰方向的向量。Σ为m×n的对角矩阵，由下式定义：

(4)

式中:0为零矩阵；
p为min(m,n)；
σp为Wv的奇异值，且σ1≥σ2≥…≥σp≥0，其反映的是U中相应干扰方向向量的权重，即奇异值越大，相应方向干扰成分占比越大；
m和n分别取值为1024和14。

2.3.2 标定环境条件干扰方向向量

选定信号环境条件干扰的去除阶次r，标定U中前r个列向量为环境条件干扰方向向量。由于U中列向量具有正交性，r值需根据独立的环境影响因素数量确定。本文测试信号的主要干扰来源于环境温湿度两个因素的变化，故r值取为2。

2.3.3 去除环境条件干扰

标定环境条件干扰方向向量后，对测试得到一待处理信号进行干扰去除，先对其进行去零均值化和单位化处理，并记为w，按下式依次去除信号w在各个标定干扰方向向量ui上的投影：

w′=w-cos(w,ui)×uii=1,2,…,r

(5)

式中:w′为去除环境条件干扰后的信号；
cos(w,ui)为w与ui的方向余弦。

笔者算法意义可理解为将测试信号偏转至参考信号的环境条件所对应的高维空间方向上，以去除环境条件变化的影响。此外应注意，为使得数据具有可比性，对去除环境条件干扰后的信号均重新进行了单位化。

3.1 超声测试信号的干扰来源

3.1.1 两片试验梁信号波动的相关性

为探究超声测试信号的干扰来源，笔者采用了与文献[14]同样的思路，对两片邻近位置的试验梁同步进行超声测试，理论假设认为两者的测试结果变化趋势具有一致性，原因在于两者处于同一环境干扰条件下。因此针对每片试验梁，计算其每组试验中14条单天样本数据两两之间的信号波动指标，以此计算结果为依据，分析两片试验梁信号波动的相关性，如图4所示。

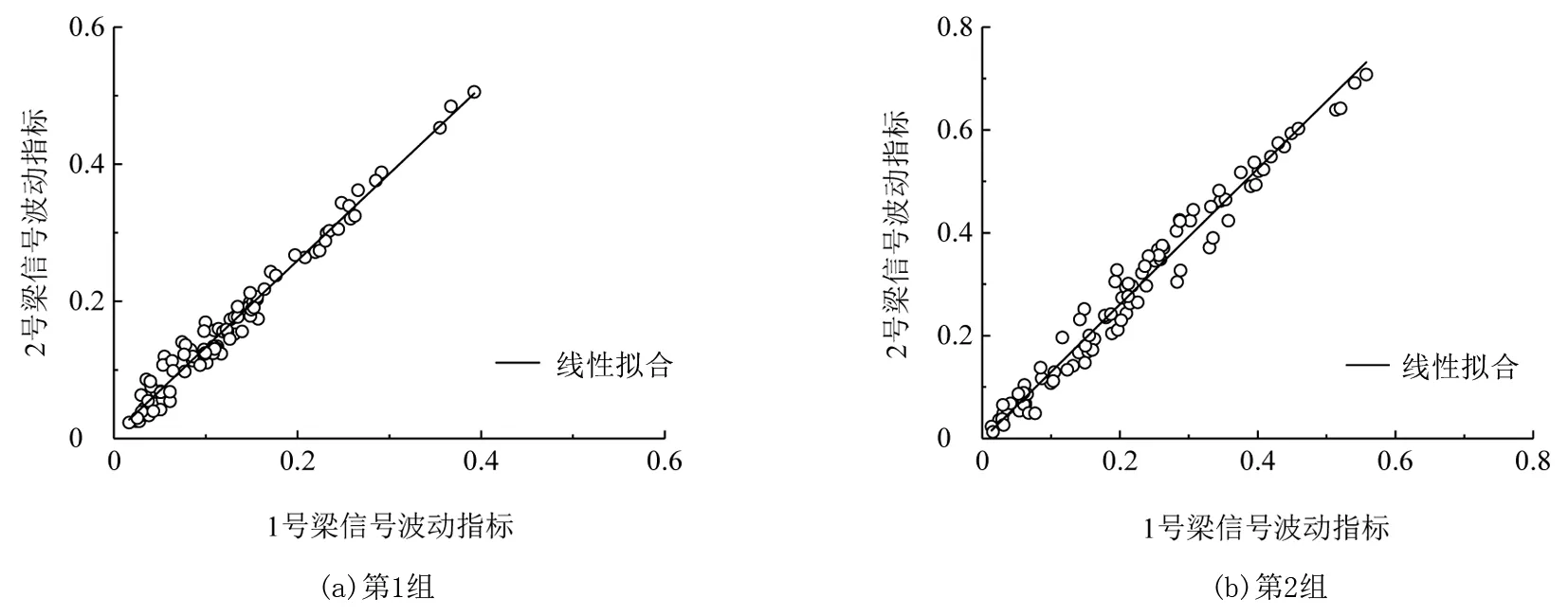
图4 两片试验梁信号波动的相关性Fig.4 Correlation of signal fluctuations of two test beams

由图4可知，两组试验中，两片试验梁信号波动指标均表现出良好的相关性，其相关系数可达0.99，显著性分析值低于0.05，这种高度相关性反映两片试验梁测试信号的波动趋势具有一致性，表明两者信号受到相同的主要因素干扰，这与本文的理论假设是一致的。而两片试验梁信号波动程度存在微小的差别，这是由于试验梁微观结构和仪器等因素具有差异。另外，由于两片试验梁信号波动的高度相关性，下文分析两者的结果是基本一致的，故仅以1号梁为例。

3.1.2 环境温湿度变化对信号波动的影响

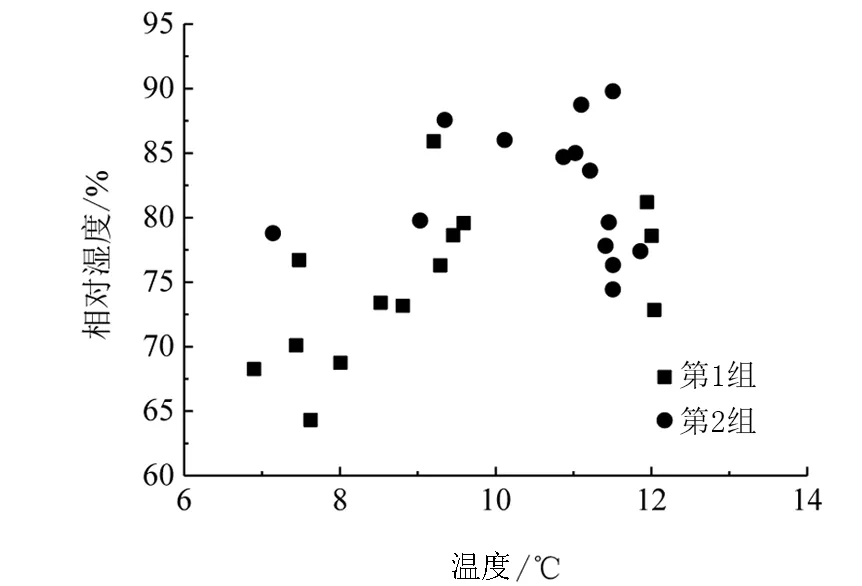
图5 试验环境温湿度变化散点图Fig.5 Scatter plot of temperature and humidity changes in the test environment

上节分析得知两片试验梁受到相同的主要干扰源影响，本节进一步分析环境条件中共同变量(即温湿度)对信号波动的影响。为减小另一变量对分析结果的干扰，采用多样本平均方法分别分析环境温度与湿度变化对信号波动的影响。图5为两组试验的环境温湿度变化情况，图中每一数据点代表单天的平均温度与平均相对湿度。可以看出，两组试验数据的环境温湿度变化区间是基本相同的，故可在分析时将两组试验数据合并考虑，以两组试验数据相应的温度和湿度中心点为基准点(温度基准为9℃，湿度基准为77.5%)，逐步扩大温度和湿度变化范围，选取对应的单天样本数据，分析不同温度和湿度变化范围内的信号波动性，结果如图6所示。图6中纵坐标为每一范围内所有单天样本数据信号波动指标(相对于其所在范围的平均波形数据)的平均值。需要说明的是，温湿度变化范围的扩大步长分别为±0.5℃和±3%，选取湿度变化范围的数据样本时仅选取温度段为11～12℃的数据，以减小温度的影响。

图6 环境温湿度变化对信号波动的影响Fig.6 The influence of ambient temperature and humidity change on signal fluctuation

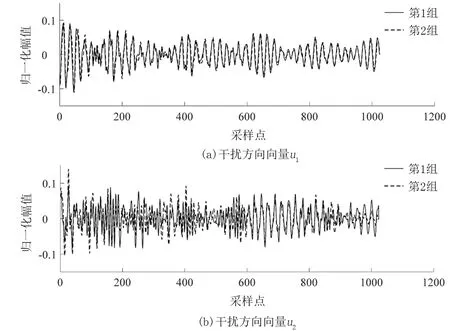
图7 两组试验干扰方向向量的波形图对比Fig.7 Comparison of waveforms of interference direction vectors between two groups of tests

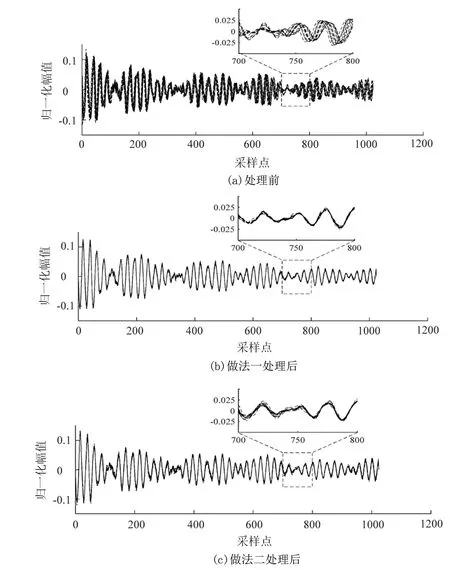
图8 算法处理前后信号的波形图对比Fig.8 Comparison of waveforms of signals before and after algorithm processing

由图6可知，信号波动指标平均值随环境温度或湿度变化范围的增大而增大，即整体上，环境温度或湿度变化越剧烈，信号的波动也将越大。且对比分析图6(a)与图6(b)中的数据可知，相较环境温度变化而言，湿度的变化对信号波动影响略小，即表明环境温度变化是超声测试信号干扰的主要来源，湿度变化为次要来源，这与文献[8,14]研究的结果是一致的，温度变化是影响混凝土超声应力测试的主要因素。

3.2 算法处理效果

3.2.1 两组试验数据的干扰方向向量比较

由于两组试验数据所对应的环境温湿度变化区间基本相同，根据笔者算法残差矩阵的构造原理，两者的干扰方向向量应该是相似的，这实质上决定了算法的正确性。故分别构造每组试验14条单天样本数据的残差矩阵，分析比较两组试验数据所标定的干扰方向向量，依据上文分析，信号干扰去除阶次r取2(即考虑环境温度和湿度两个信号干扰因素)，两组试验数据的干扰方向向量的波形图如图7所示。

由图7(a)可知，两组试验数据的干扰方向向量u1的波形较为接近。相较而言，由图7(b)可知，两者的干扰方向向量u2的波形差别较大，这是因为u2方向上的干扰成分占比较低，但波形的总体走势基本是相同的。这表明在误差范围内两组试验数据所标定的干扰方向向量是基本一致的，而两者的差异是由于两组试验数据所对应的温湿度区间不完全一致造成的。由此检验了笔者所建立的信号环境温湿度干扰去除算法的正确性。

3.2.2 算法处理前后信号波动性对比

本节对算法的有效性进行多层次检验，检验分两种做法，分别为：做法一，首先每组试验单天样本数据去除其各自标定的干扰方向向量上的投影；
做法二，在做法一基础上，以其中一组(可视为训练组)试验数据标定环境条件干扰方向向量，另一组(可视为测试组)试验数据去除在该标定的干扰方向向量上的投影。算法处理效果由图8、图9描述，图8和图9分别为算法处理前后信号归一化波形对比图与信号波动指标对比图，需要说明的是，图8的结果仅以第1组试验14条单天样本数据的结果为例进行分析，图9中的信号波动指标为单天样本超声数据相对于其组内总平均数据的计算结果。

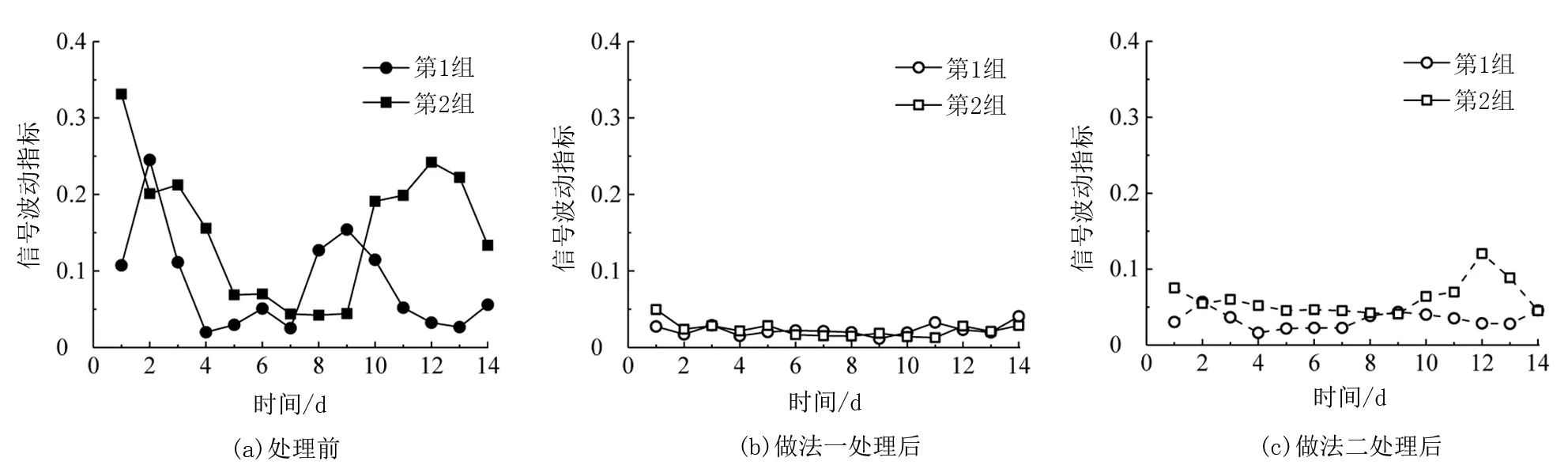
图9 算法处理前后信号波动指标对比Fig.9 Comparison of signal fluctuation index before and after algorithm processing

由图8可知，相较于处理前，经过做法一处理后，信号的波形变得更加平滑，带宽明显变窄，波形之间差异有明显的降低，且保留了大部分信息，得到了稳定性和可重复性较好的试验数据。而做法二处理后同样能取得较好的效果，但相较做法一，其波形之间的差别稍大，处理效果略差，这是由两组试验数据对应的测试环境温湿度区间存在微小差异造成的。

进一步分析图9中的数据可知，平均意义上，两组试验数据处理前信号波动指标为0.135。经过做法一处理后，信号波动指标下降至0.023，而经过做法二处理后下降至0.047，降幅分别约为83%和65%，这与图8的分析结果是一致的。因此，本文算法可有效去除信号的温湿度干扰，减小信号的波动性，总体上，信号波动指标约从0.14降低至0.05，降幅超过50%。略为遗憾的是，文中算法的有效性仅建立在环境温度变化|ΔT|小于3℃，且相对湿度变化|ΔHr|小于12.5%条件下，这是由于本文所采集的数据仅在此变化范围内。而当环境温湿度变化超出此范围，实际上可对信号进行小温湿度区间划分，每个小变化区间内的信号先独立通过算法去除温湿度干扰，而后再次重新划分温湿度区间并进行处理，以此逐步的降低温湿度变化影响，最后可将所有信号偏转至同一温湿度下所对应的高维空间方向上。理论上，根据这种类似于局部线性化的思想，可对超过上述的温湿度变化区间的信号进行处理，由于此内容不是本文重点，待后期另行撰文分析。

研究混凝土梁超声测试信号的温湿度干扰去除算法。在环境温湿度自然变化的室内条件下，开展两片混凝土工字梁超声测试，通过构造的信号波动指标分析两者相关性，判断信号是否含有相同的干扰成分。分析环境温湿度变化对信号波动的影响，针对性建立一种基于残差矩阵SVD的信号干扰去除算法，获得稳定性较好的超声尾波信号，为后续混凝土结构应力测量方法的研究创造条件。主要如下结论：

1)两片试验梁的信号波动指标表现出良好的相关性(相关系数为0.99)，表明两者信号主要受到相同的干扰因素影响。

2)总体上，环境温度或湿度变化越大，信号波动越大，其中温度变化是信号干扰的主要来源，湿度变化为次要来源。

3)在试验环境温湿度变化的全域内(|ΔT|<3℃与|ΔHr|<12.5%)，针对超声尾波信号的温湿度干扰去除问题，本文建立的算法在混凝土工字梁上得到验证，信号波动指标从原来的0.14降低至0.05，降幅超过50%。

猜你喜欢温湿度波动向量向量的分解新高考·高一数学(2022年3期)2022-04-28温湿度控制器在回收砂冷却系统中的应用装备制造技术(2021年5期)2021-08-14聚焦“向量与三角”创新题中学生数理化(高中版.高考数学)(2021年1期)2021-03-19基于DSP的多路温湿度监测系统漳州职业技术学院学报(2019年1期)2019-11-16羊肉价回稳 后期不会大幅波动今日农业(2019年12期)2019-08-13微风里优美地波动文学少年(原创儿童文学)(2019年1期)2019-05-232019年国内外油价或将波动加剧中国化肥信息(2019年3期)2019-04-25基于温湿度控制的天气预测装置电子制作(2018年11期)2018-08-04干湿法SO2排放波动对比及分析环境保护与循环经济(2017年2期)2017-09-26蒸发冷却温湿度独立控制空调系统的应用西安工程大学学报(2016年6期)2017-01-15